ПэЧэ и КуРу (p-адические числа и кубик Рубика)

однажды элементарные понятия абстрактной алгебры помогли мне собрать кубик рубика, который никак не собирался исходя из "здравого смысла" (слишком сложно было "увидеть" решение)

подумал, что изучение p-адических чисел можно превратить в игру и развлечение на основе идеи кубика Рубика

итак, читаем вики https://ru.wikipedia.org/wiki/Группа_кубика_Рубика

-----------------------------

Гру́ппа ку́бика Ру́бика — подгруппа симметрической группы S<sub>48

...</sub>

Порядок группы ${\displaystyle G}$ равен^{[2][3][4][5][6]}

${\displaystyle |G|={\dfrac {8!\cdot 12!\cdot 3^{8}\cdot 2^{12}}{3\cdot 2\cdot 2}}=43\ 252\ 003\ 274\ 489\ 856\ 000=2^{27}\cdot 3^{14}\cdot 5^{3}\cdot 7^{2}\cdot 11.}$

Пусть ${\displaystyle K_{f}}$ — граф Кэли группы ${\displaystyle G}$ с 18 образующими, которые соответствуют 18 ходам метрики FTM.

Каждая из ${\displaystyle \approx 4{,}32\cdot 10^{19}}$ конфигураций может быть решена не более чем за 20 ходов FTM. Другими словами, эксцентриситет вершины графа ${\displaystyle K_{f}}$, соответствующей «собранному» состоянию головоломки, равен 20^[7].

Диаметр графа ${\displaystyle K_{f}}$ также равен 20^[8].

-----------------------------

грубо говоря, интуитивно РАССТОЯНИЕ для КР - это минимальное число поворотов, за которое он собирается  (максимальное - это 20)

-------------------------------

9 сентября 2010 в 00:56

Разработка → Кубик Рубика за 20 шагов

https://habrahabr.ru/post/103843/

Любая позиция Кубика Рубика может быть решена не более, чем за 20 шагов.

Несколько лет назад было доказано, что для Кубика Рубика есть решение за 23 хода. Теперь это число сократилось до 20. Чтобы это сделать, потребовалось 35 (тридцать пять) лет компьютерного времени, пожертвованного Гуглом.


Каждый блок решения использовал свой алгоритм — последовательность шагов для достижения нужной конфигурации. Например, один алгоритм предназначался для решения верхней грани, а другой — для позиционирования средних краев. Есть множество различных алгоритмов, различающихся по степени сложности и количеству требуемых шагов, но те, которые может запомнить человек, обычно требуют больше 40 шагов.

Разумно полагать, что Бог может использовать более эффективный алгоритм, который решает задачу за наикратчайшее число шагов. Этот алгоритм известен как “алгоритм Бога”. Число шагов в худшем случае называется числом Бога. В конце концов, было показано, что это число — 20.

После изобретения Кубика Рубика пятнадцать лет ушло на поиск позиции, которая наверняка решается за 20 шагов. Через 15 лет после этого мы докажем, что 20 шагов достаточно для любой позиции.

История числа Бога

К 1980 году было установлено, нижняя граница — 18, а верхняя — вероятно, около 80. В таблице ниже собраны все результаты:

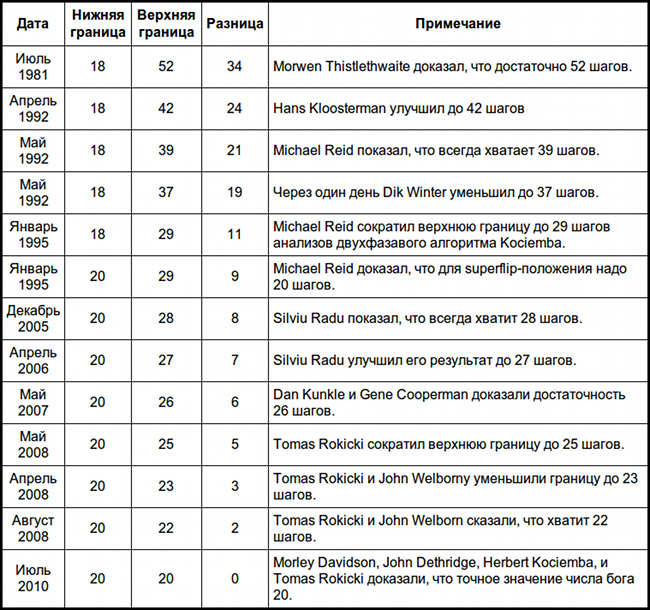
Как мы это сделали

Как мы справились с 43 252 003 274 489 856 000 позициями Кубика Рубика?

• Мы разделили все позиции на 2 217 093 120 множеств — по 19 508 428 800 позиций в каждом.
• Мы уменьшили число множеств для решения до 55 888 296 на основе симметрии и покрытии множества.
• Мы не искали оптимальное решение, а только решения с длиной 20 или менее шагов.
• Мы написали программу, находящее решение для одного множества за 20 секунд.
• Потребовалось 35 лет компьютерного времени для поиска решений всех конфигураций в каждом из 55 888 296 множеств.

Деление пространства позиций

Мы разбили большую задачу на 2 217 093 120 меньших подзадач: в каждую входило по 19,508,428,800 различных позиций. Одна такая подзадача легко помещается в память современного компьютера, и этот метод позволил достаточно быстро получить решение.

Симметрия

Если повертеть Кубик Рубика влево-вправо или вверх-вниз, то, по сути, ничего не изменится: число шагов в решении останется тем же самым. Вместо того, чтобы решать все эти позиции, можно получить решение для одной и распространить его на повернутые позиции. Есть 24 различных ориентации в пространстве и 2 зеркальных положения Кубика для каждой позиции, что позволяет уменьшить число решаемых позиций в 48 раз. Если использовать аналогичные рассуждения и воспользоваться поиском задачи “покрытия множества”, то число подзадач уменьшается от 2 217 093 120 до 55 882 296.

Хорошие и оптимальные решения

Оптимальное решение содержит достаточное количество шагов, но не больше, чем надо. Так как уже известна одна позиция, для которой требуется 20 шагов, то мы можем не искать оптимальное решение для каждой позиции, а только решения в 20 или менее шагов. Это многократно убыстряет задачу.

Оборудование

У нас была возможность решить 55 882 296 подзадач на мощностях Гугла и выполнить все вычисления за несколько недель. Гугл не раскрывает характеристики компьютеров, но было затрачено 1.1 миллиард секунд компьютерного времени (Intel Nehalem, four-core, 2.8GHz) на выполнение расчетов.

Самая трудная позииция

Мы знали в течении 15 лет, что есть позиции, которые требует 20 шагов, но мы доказали, что ни для одной позиции и не надо больше.

Позиции с решениями в 20 шагов редки, но их вполне возможно встретить в реальности. Вероятность встретить такую позицию варьируется от 10^(-9) до 10^(-8). Мы точно не знаем точное количество таких позиций. Таблица дает оценку числа позиций для каждой длины решения.
 

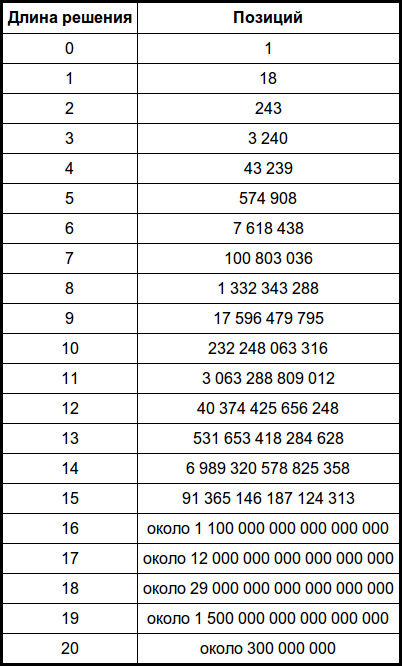
Для длин от 16 и больше, числа являются примерными. Наши исследования подтвердили все первоначальные данные до 14 строки включительно, а 15 строка — новый результат. На 11 августа мы обнаружили 12 миллионов позиций с длиной решения 20. Эта позиция была самой сложной для наших программ:

---------------------------

теперь попробуем сформулировать проблему в терминах ПэЧэ

с учётом степеней свободы и того, что поворот навлево равен трём поворотам направо мы можем построить 5-адическое дерево для всех возможных переходов (одну грань можно считать фиксированной и крутить только 5 остальных)

на этом дереве 5-адических чисел вводим отображение (функцию) и "расстояние"

любая "загогулина" на этом дереве (ПэЧэ), повторенная определенное число раз, возвращает чило "к себе" (визуально можно представить себе стрелочки в обратную сторону)

получается что-то типа  неориентированного графа - как в детской игре - когда бросают кости, выпадает число, игрок шагает по карте (тропинка с позициями) и там есть "хитрые места", где игрок "телепортируется" в другое место (задача игру - попасть точно в "выигрышную" позицию "финиш")

игру можно переделать в форму "бродилки со стрелками телепортации"

на 5-адическом дереве для любой "загогулины" (кусочка пути) вводится автоматический эффект телепортации - "возврат в исходную позицию" (задаётся формулой, матрицей или графом) - целочисленная фонкция от "загогулины" - сколько раз нужно повторить "заггогулину", чтобы вернуться в ту же позицию

на полпути "траектория" возврата почти соприкасается с исходной точкой - именно это позволило найти путь к сборке (не самый короткое но всё же решение)

короче, цель головоломки - за минимально число шагов (20 шагов - это вроде с возможностью поворачивать в обе стороны и на 180 градусов - т.е. для 5-алического дерева наверно нужно не больше 52 движений ? ) с учётом автоматической "телепортации" с любой ветки "слезть на землю" (т.е. очутиться в корне 5-адического дерева)

тут можно даже игру бродилку нарисовать - пусть дети с малолетства приучаются мыслить в адических понятиях о расстоянии

ибо как говорил Козьма Прутков - "Бросая в воду камешки, смотри на круги, ими образуемые; иначе такое бросание будет пустою забавою.":-)